Probabilidade: O que é? Definições, História e Tipos de Probabilidades.

A probabilidade é um campo da matemática que estuda as chances numéricas de um evento ocorrer num experimento aleatório. Onde experimento aleatório é aquele experimento que, quando repetido em iguais condições, pode fornecer resultados diferentes.

É uma ferramenta usada e necessária para fazer ligações entre a amostra e a população, de modo que, a partir de informações da amostra, possam ser feitas afirmações sobre características da população.

Refere-se ao estudo das chances de ocorrência de um resultado, que são obtidas pela razão entre casos favoráveis e casos possíveis.

Por José Sérgio Marcondes.
Postado 02/06/2020

1. História, Origem a Probabilidade

No ano de 1654, um jogador da sociedade parisiense chamado Chevalier de Mére propôs ao matemático Blaise Pascal algumas questões sobre possibilidades de vencer jogos. Uma dessas questões foi:

“Um jogo de dados entre dois adversários chega ao fim quando um dos jogadores vence três partidas em primeiro lugar. Se esse jogo for interrompido antes do final, de que maneira cada um dos jogadores deverá ser indenizado?”

As reflexões em torno destes problemas levaram Pascal a corresponder-se com Pierre de Fermat, desencadeando discussões a respeito dos princípios de uma nova teoria, que veio a ser chamada Teoria da Probabilidade.

Em condições normais podemos prever a que temperatura o leite ferve, por exemplo. Esse tipo de experimento, cujo resultado é previsível, recebe o nome de experimento determinístico.

Esse tipo de experimento, cujo resultado não pode ser previsto, é chamado de experimento aleatório.

2. O que é Experimento Aleatório?

Experimento aleatório é aquele experimento que, quando repetido em iguais condições, pode fornecer resultados diferentes, ou seja, são resultados explicados ao acaso, isto é, não podem ser previamente determinados, dependem exclusivamente do acaso.

Se o fenômeno seguir um modelo não determinístico, temos um experimento aleatório que apresentam características expecíficas.

2.1 Características do Experimento Aleatório.

• O experimento pode ser repetido;
• Embora não seja possível afirmar que resultado em particular ocorrerá, é possível descrever o conjunto de todos os resultados possíveis do experimento; e
• À medida que aumenta o número de repetições aparece uma certa regularidade que torna possível a construção de um modelo matemático.

2.1 Exemplo de Experimento Aleatório:

• Lançamento de dois dados;
• Lançamento de uma moeda; e
• Sorteio de um cupom dentre cem mil cupons, etc.

Observação: Na teoria das probabilidades, estudamos os experimentos aleatórios equiprováveis, ou seja, aqueles em que qualquer resultado pode ocorrer com a mesma chance. É o caso do lançamento de uma moeda: a possibilidade de ocorrer cara ou coroa é a mesma.

3. Espaço Amostral da Probabilidade

Espaço amostral é o conjunto universo ou o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral é S.

3.1 Exemplos espaço amostral:

1. No experimento “lançamento de um dado” e observar a face superior temos como espaço amostral o conjunto S = {1, 2, 3, 4, 5, 6}. Portanto: n (S) = 6.
2. Num jogo de futebol, entre duas equipes, uma das equipes pode obter resultados tais como: vitória (v), empate (e) ou derrota (d). Tem-se então: S = {v, e, d}. Portanto: n (S) = 3

4. Evento da Probabilidade

Na probabilidade Evento é um conjunto qualquer de resultados de um experimento aleatório. Pode-se dizer que um evento é qualquer subconjunto de um espaço amostral. É representado, pela letra E.

4.1 Exemplo de evento:

No lançamento de duas moedas, o espaço amostral é E = {(C,C), (C,K), (K,C), (K,K)}.

Se aparecer faces iguais, o conjunto C = {(K,K), (C,C)}, subconjunto de E, é um evento de E.

4.2 Tipos de eventos na probabilidade:

• Eventos certos;
• Eventos impossíveis;
• Eventos elementares; e
• Evento complementar.

a) Eventos certos:

Na probabilidade eventos certos são eventos que possuem todos os elementos do espaço amostral.

Logo, se E = S, ele é o próprio espaço amostral.

Exemplo: Lançamento de um dado e ocorrência de um número menor do que 6 na face superior.

b) Eventos impossíveis:

Os eventos impossíveis são eventos que não possuem elementos no espaço amostral.

Logo, se E = Ø, o evento E é chamado de evento impossível.

Exemplo: Lançamento de um dado e ocorrência de um número maior do que 6 na face superior.

c) Eventos elementares:

Eventos elementares – se E ⊂ S (E está contido em S) e E é um conjunto
unitário, então E é chamado evento elementar.

Exemplo:Lançamento de um dado e ocorrência de um número ímpar maior do que 4 na face superior.

d) Evento complementar:

Em relação a determinado evento A, podemosdefinir seu evento complementar (A) que é caracterizado pela não ocorrência daquele evento.

Exemplo: Considerando o lançamento de um dado, onde S = {1, 2, 3, 4, 5, 6}, e definido o evento A = {números pares}, então o evento complementar de A é o conjunto dos números ímpares, A = {1, 3, 5}.

A probabilidade de um evento ocorrer num experimento aleatório equiprovável é dada pelo quociente da divisão do número de casos favoráveis pelo número de casos possíveis.

5. Definição e Conceito de Probabilidade

A probabilidade é um campo da matemática que estuda as chances numéricas de um evento ocorrer num experimento aleatório ou a possibilidade de uma proposição ser verdadeira.

É uma ferramenta usada e necessária para fazer ligações entre a amostra e a população, de modo que, a partir de informações da amostra, possam ser feitas afirmações sobre características da população.

A palavra probabilidade deriva do Latim probare (provar ou testar).

De acordo com o dicionário, probabilidade é um substantivo feminino que indica perspectiva favorável de que algo venha a ocorrer; possibilidade, chance.

De acordo com Levine (2008), probabilidade é um valor numérico que representa uma chance, uma eventualidade ou uma possibilidade de que um determinado evento venha a acontecer.

Refere-se ao grau de segurança com que se pode esperar a realização de um evento, determinado pela frequência relativa dos eventos do mesmo tipo numa série de tentativas.

A probabilidade é o número de vezes que um determinado evento
pode ocorrer em num experimento aleatório.

Probabilidade é o estudo das chances de ocorrência de um resultado, que são obtidas pela razão entre casos favoráveis e casos possíveis.

Se em um fenômeno aleatório as possibilidades são igualmente prováveis,
então a probabilidade de ocorrer o evento A é:

5.1 Exemplo probabilidade:

No lançamento de um dado, um número para pode ocorrer de 3 maneiras diferentes, dentre 6 igualmente prováveis, portanto, P= 3/6 = ½ = 50%.

Dizemos que um espaço amostral S (finito) é equiprovável quando seus eventos elementares têm probabilidades iguais de ocorrência.

Num espaço amostral equiprovável S (finitos), a probabilidade de ocorrência de um evento A é sempre:

5.2 Exemplo probabilidade:

Fazendo-se inspeção em um lote de 240 peças de motor, o departamento de controle de qualidade constatou que 20 peças estavam com defeito. Retirando-se ao acaso uma das 240 peças, a probabilidade de esta peça NÃO ser defeituosa é:

• Sendo S o conjunto dos elementos do espaço amostral, casos possíveis, e n (S) o número de elementos deste conjunto.
• Sendo A o conjunto dos elementos das peças defeituosas, e n (A) o número de elementos deste conjunto.
• Sendo E’ o conjunto dos elementos das peças não defeituosas, e n (E’) o número de elementos deste conjunto. Neste caso, é o conjunto dos casos favoráveis.

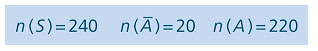
Para calcular a probabilildade de retirada de uma peça que seja não defeituosa, faça assim:

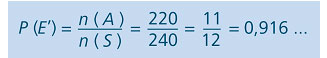
Isso significa que a probabilidade de retirar uma peça não defeituosa é de 91,6% aproximadamente.

6. Eventos complementares

Se A e A são eventos complementares, então:

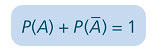
7. Probabilidade condicional

Antes da realização de um experimento, é necessário que já se tenha alguma informação sobre o evento que se deseja observar. Nesse caso, o espaço amostral se modifica e o evento tem a sua probabilidade de ocorrência alterada.

7.1 Fórmula da probabilidade condicional:

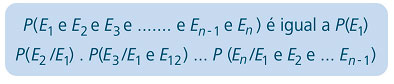
Onde:

P (E2/E1) é a probabilidade de ocorrer E2 condicionada pelo fato de já ter
ocorrido E1;

P (E3/E1 e E2) é a probabilidade de ocorrer E3, condicionada pelo fato de já
terem ocorrido E1 e E2;

P (En/E1 e E2 e… En-1) é a probabilidade de ocorrer En, condicionada ao fato de já ter ocorrido E1 e E2… En-1.

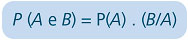
7.2 Exemplo probabilidade condicional

Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez e sem reposição, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?

Seja o espaço amostral S = 30 bolas e consideramos os seguintes eventos:

A: vermelha na primeira retirada e P(A) = 10/30

B: azul na segunda retirada e P(B) = 20/29

Assim:

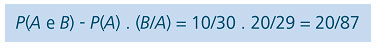
8. Eventos independentes

Dizemos que E1 e E2 e… En-1 são eventos independentes quando a probabilidade de ocorrer um deles não depende do fato de os outros terem ou não terem ocorrido.

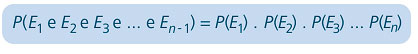
8.1 Exemplo probabilidade em eventos independentes

Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas uma de cada vez e repondo a sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?

Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na segunda retirada é igual ao produto das probabilidades de cada condição, ou seja, P(A e B) = P(A) . P(B).

Ora, a probabilidade de sair vermelha na primeira retirada é 10/30 e a de sair azul na segunda retirada 20/30. Daí, usando a regra do produto temos:

Observe que na segunda retirada foram consideradas todas as bolas, pois houve reposição. Assim, P(B/A) = P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que ela foi reposta na urna.

9. Probabilidade de ocorrer a união de eventos

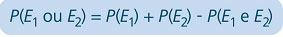
De fato, se existirem elementos comuns a E1 e E2, estes eventos estarão computados no cálculo de P(E1) e P(E2). Para que sejam considerados uma vez só, subtraímos P(E1 e E2).

Probabilidade de ocorrer união de eventos mutuamente exclusivos:

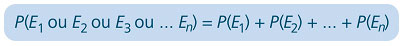
Exemplos:

A) Se dois dados, azul e branco, forem lançados, qual a probabilidade de sair 5 no azul e 3 no branco?

Considerando os eventos:

A: Tirar 5 no dado azul e P(A) = 1/6

B: Tirar 3 no dado branco e P(B) = 1/6

Sendo S o espaço amostras de todos os possíveis resultados, temos:

Daí temos:

B) Se retirarmos aleatoriamente uma carta de um baralho com 52 cartas, qual a probabilidade de ser um 8 ou um rei?

Sendo S o espaço amostral de todos os resultados possíveis, temos: n(S) = 52 cartas.

Considere os eventos:

A: Sair 8 e P(A) = 4/52

B: Sair um rei e P(B) = 4/52

Assim, P(A ou B) = 4/52 + 4/52 – 0 = 8/52 = 2/13

Note que P(A e B) = 0, pois uma carta não pode ser 8 e rei ao mesmo tempo.

Observação: Quando isso ocorre, A ∩ B = ø, dizemos que os eventos A e B são mutuamente exclusivos.

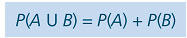
10. Dúvidas frequentes sobre probabilidade

10.1 Qual é a fórmula da Probabilidade?

Em um fenômeno aleatório, as possibilidades de ocorrência de um evento são igualmente prováveis. Sendo assim, podemos encontrar a probabilidade de ocorrer um determinado resultado através da divisão entre o número de eventos favoráveis e o número total de resultados possíveis:

p(A)=n(A)/n(∩)

Sendo:

p(A): probabilidade da ocorrência de um evento A
n(A): número de casos que nos interessam (evento A)
n(Ω): número total de casos possíveis

10.2 Quais são os três tipos de estatistificas?

• Probabilidade clássica: usada quando cada resultado no espaço amostral tem a mesma probabilidade de ocorrer. A probabilidade é baseada no conhecimento prévio do processo envolvido.
• Probabilidade empírica: baseia-se em observações obtidas de experimentos aleatórios. Os resultados são baseados em dados observados e não no conhecimento prévio do processo.
• Probabilidade subjetiva, intuição estimativa ou palpite: normalmente baseada em experiência no passado, opinião pessoal ou análise de algum indivíduo. Pode ser útil, quando não há possibilidade de utilização da probabilidade clássica ou empírica.

10.3 Definições

• Experimento ou Fenômeno Aleatório – São aqueles que, mesmo repetidos várias vezes sob condições semelhantes, apresentam resultados imprevisíveis.
• Espaço Amostral: é o conjunto de possíveis resultados de um experimento ou fenômeno aleatório, representado por S.
• Evento: é qualquer subconjunto do espaço amostral S de um evento aleatório.

11. Você Gostou? Sem sim, colabore com o crescimento do Blog

Para continuar publicando e disponibilizando os artigos de forma gratuita a todos, solicito a você leitor ou leitora, que ajude na divulgação e crescimento do blog, fazendo pelo menos uma das práticas a seguir:

• Deixe seu comentário no final do artigo, ele é muito importante para nós;
• Divulgue, curta e compartilhe as publicações com seus amigos pelas redes sociais;
• Leia mais um artigo, essa prática nos ajuda muito;
• Inscreve-se na nossa Newsletter.

Convido você a se inscrever para acompanhar as publicações do nosso blog, os links para cadastro estão na lateral do blog para acessos com desktop ou logo abaixo para acessos com celular.

Obrigado pelo tempo disponibilizado na leitura de nosso artigo, espero que tenha sido útil pra você!

Forte abraço e sucesso!

José Sérgio Marcondes

Acesse o botão a seguir e você encontrará uma lista de posts relacionados ao tema desse post, que lhe serão muito úteis como leitura complementar a esse assunto. Quero saber mais sobre esse assunto.

12. Dados para Citação em Trabalhos

MARCONDES, José Sérgio (27 de abril de 2020).Balanced Scorecard (BSC) O que é? Objetivos, Pilares, Perspectivas. Disponível em Blog Gestão de Segurança Privada: – Acessado em (inserir data do acesso).

13. Referencias Bibliográficas

Costa, Paulo Roberto da Estatística / Paulo Roberto da Costa. – 3. ed. – Santa Maria : Universidade Federal de Santa Maria, Colégio Técnico Industrial de Santa Maria, Curso Técnico em Automação Industrial, 2011.

COSTA NETO, P. L. de O. Probabilidades. 2. ed. São Paulo: Editora Edgard Blucher Ltda, 2005.

COSTA NETO, P. L. de O. Estatística. São Paulo: Editora Edgard Blucher Ltda, 2002.