O que é Estimativa de Probabilidades na Avaliação de Riscos?

A estimativa de probabilidades desempenha um papel crucial na avaliação de riscos, sendo um dos pilares fundamentais da gestão de riscos em diversos setores. Essa prática consiste em quantificar a chance de um evento adverso ocorrer, permitindo que organizações e profissionais antecipem possíveis cenários e implementem medidas de mitigação eficazes. Em um ambiente de constante incerteza, entender como as probabilidades podem ser aplicadas torna-se uma habilidade indispensável para a tomada de decisões estratégicas.

Ao determinar a probabilidade de um risco, é possível priorizar as ameaças com maior chance de impacto. Isso não apenas facilita a alocação de recursos de maneira mais eficiente, mas também assegura que esforços sejam concentrados onde realmente são necessários. A probabilidade é, portanto, um guia essencial para transformar incertezas em ações concretas, possibilitando decisões mais seguras e bem-informadas.

Continue lendo este artigo para entender as principais abordagens, metodologias e exemplos práticos sobre como estimar probabilidades na avaliação de riscos.

O que é Estimativa de Probabilidades na Avaliação de Riscos?

A estimativa de probabilidades na avaliação de riscos refere-se ao processo de quantificar a chance de ocorrência de eventos adversos em um determinado contexto. Em termos simples, trata-se de atribuir uma probabilidade a um risco específico, permitindo que ele seja melhor compreendido e gerenciado. Esse conceito é amplamente aplicado em diversas áreas, como finanças, engenharia, saúde, segurança corporativa e muitos outros setores onde a avaliação de riscos desempenha um papel central na estratégia organizacional.

No campo da gestão de riscos, a estimativa de probabilidades é um processo essencial para compreender e mensurar incertezas. Ao utilizar técnicas qualitativas e quantitativas para determinar a probabilidade de um evento, as organizações conseguem mapear possíveis cenários e priorizar ações de tratamento de riscos. Esse processo não apenas contribui para a redução de incertezas, mas também para uma análise mais objetiva e fundamentada dos riscos.

A importância dessa prática está diretamente relacionada à tomada de decisões mais seguras e estratégicas. Por meio da estimativa de probabilidades, é possível:

• Analisar e selecionar os riscos mais críticos que demandam atenção imediata.
• Desenvolver estratégias para minimizar ou eliminar ameaças potenciais.
• Direcionar recursos de maneira eficiente, evitando desperdícios.
• Melhorar a comunicação sobre os níveis de risco entre diferentes stakeholders.

Ao transformar incertezas em valores numéricos ou descritivos, a estimativa de probabilidades oferece às organizações uma base sólida para agir de forma preventiva, garantindo resiliência e adaptabilidade diante de desafios futuros. Essa prática é, portanto, um pilar para decisões mais bem informadas e alinhadas aos objetivos estratégicos.

Por que a Estimativa de Probabilidades é Importante?

A estimativa de probabilidades na avaliação de riscos é uma prática indispensável para qualquer organização que busca eficiência, segurança e estratégias robustas. Seu impacto vai muito além de simplesmente quantificar incertezas; ela serve como base para uma série de decisões críticas. Entenda as razões pelas quais essa prática é tão importante.

1. Priorização de Riscos: Nem todos os riscos apresentam o mesmo nível de ameaça ou probabilidade de ocorrer. A estimativa de probabilidades ajuda as organizações a identificar os riscos mais críticos, que exigem atenção prioritária.
2. Tomada de Decisão Informada: A incerteza é uma das maiores inimigas de decisões eficazes. Quando se atribui uma probabilidade a um risco, é possível tomar decisões com base em dados concretos e previsões fundamentadas.
3. Eficiência na Alocação de Recursos: Recursos como tempo, capital e mão de obra são limitados. A estimativa de probabilidades permite direcionar esses recursos de forma eficiente, garantindo que sejam aplicados onde há maior necessidade.
4. Facilitação da Comunicação entre Stakeholders: Uma das grandes vantagens da estimativa de probabilidades é a sua capacidade de traduzir riscos em linguagem compreensível para diferentes públicos, desde gestores até investidores e equipes operacionais. Ao apresentar dados claros e objetivos, as organizações conseguem engajar stakeholders, promovendo um entendimento compartilhado sobre as prioridades e ações necessárias.

Principais Abordagens para Estimar Probabilidades

A estimativa de probabilidades na avaliação de riscos pode ser realizada por meio de diferentes abordagens, cada uma adaptada às características do risco analisado e à disponibilidade de dados. Aqui, destacamos três métodos amplamente utilizados: a utilização de dados históricos, técnicas preditivas e o julgamento de especialistas.

1. Utilização de Dados Históricos para Estimativa de Probabilidades

Os dados históricos são uma das ferramentas mais confiáveis para prever a probabilidade de eventos futuros. Analisando ocorrências passadas de situações semelhantes, é possível identificar padrões que ajudam a antecipar riscos. Por exemplo, uma empresa pode consultar registros de falhas de equipamentos ou incidentes de segurança para determinar a probabilidade de novos eventos similares.

No entanto, essa abordagem possui limitações significativas:

• Baixa frequência de eventos: Quando os eventos são raros, as estimativas podem ser menos precisas. Por exemplo, em riscos catastróficos que quase nunca ocorrem, a escassez de dados compromete a confiabilidade das previsões.
• Ausência de dados anteriores: Em situações inéditas, onde não há registros históricos, essa abordagem torna-se inviável.

Apesar disso, a utilização de dados históricos permanece essencial em cenários onde informações confiáveis estão disponíveis, oferecendo um ponto de partida sólido para a análise.

2. Técnicas Preditivas para Estimativa de Probabilidades

Quando os dados históricos são insuficientes ou inadequados, as técnicas preditivas tornam-se a principal opção para estimar probabilidades. Entre as ferramentas mais comuns estão:

• Análise Preditiva: A análise preditiva é uma técnica avançada que se baseia na aplicação de modelos estatísticos e algoritmos de inteligência artificial (IA) para analisar dados históricos e fazer previsões sobre eventos futuros.
• Análise de Árvore de Falhas: Um método que identifica possíveis falhas em sistemas e avalia a probabilidade de cada uma ocorrer. Ele é especialmente útil em engenharia e manutenção preventiva.
• Simulações: Modelos como o Método de Monte Carlo ajudam a simular cenários variados, considerando diferentes variáveis e incertezas para prever probabilidades.
• Modelos Preditivos: Ferramentas matemáticas e estatísticas que analisam dados atuais para prever eventos futuros.

Essas técnicas exigem atenção a aspectos como:

• Falhas comuns: É essencial considerar que certos eventos podem compartilhar causas comuns. Por exemplo, em sistemas interconectados, um único ponto de falha pode desencadear diversos problemas.
• Degradação e envelhecimento: Componentes e estruturas envelhecem, aumentando a probabilidade de falhas ao longo do tempo. Simulações que incorporam esses fatores são cruciais para previsões mais precisas.

3 Opinião de Especialistas na Estimativa de Probabilidades

Nos casos em que os dados históricos ou preditivos não estão disponíveis, o julgamento de especialistas desempenha um papel central na estimativa de probabilidades. Profissionais com experiência no setor analisam as informações disponíveis e oferecem insights baseados em seu conhecimento técnico.

Alguns métodos estruturados para coleta de opiniões incluem:

• Método Delphi: Um processo iterativo em que especialistas são consultados de forma anônima, e suas respostas são refinadas até alcançar um consenso.
• Classificação de Categorias: Especialistas atribuem probabilidades com base em escalas pré-definidas, como “baixa”, “média” ou “alta”.

A combinação de experiência prática e análise sistemática fortalece as estimativas, especialmente em cenários complexos. Contudo, para garantir resultados confiáveis, é importante reunir especialistas diversificados e utilizar técnicas formais de indução de julgamento.

Cada abordagem – dados históricos, técnicas preditivas e opinião de especialistas – possui vantagens e desafios específicos. A escolha do método ideal dependerá das características do risco, da disponibilidade de informações e dos recursos organizacionais. Em muitos casos, combinar essas abordagens resulta em estimativas mais robustas e precisas.

Tipos de Metodologias Empregadas na Estimativa de Probabilidades

A escolha da metodologia para estimativa de probabilidades na avaliação de riscos é um passo crucial para garantir que os resultados sejam precisos, confiáveis e adequados ao contexto analisado. Existem três categorias principais de abordagens: qualitativas, quantitativas e a combinação de ambas.

1. Abordagens Qualitativas para Estimativa de Probabilidades

As abordagens qualitativas são ideais para situações em que dados numéricos ou históricos são escassos. Elas dependem do julgamento humano, da percepção de especialistas e de métodos estruturados para atribuir valores ou categorias às probabilidades.

Exemplos de metodologias qualitativas:

• Escalas de Likert: Esta técnica utiliza uma escala numérica ou descritiva (como “baixa”, “média”, “alta”) para classificar a probabilidade de eventos. É amplamente usada pela sua simplicidade e facilidade de compreensão.
• Método Delphi: Um processo iterativo no qual especialistas compartilham opiniões de forma anônima, revisando suas respostas com base no feedback coletivo até alcançar um consenso. Essa abordagem minimiza vieses individuais e promove resultados mais robustos.
• Brainstorming: Sessões de grupo em que participantes identificam riscos potenciais e estimam suas probabilidades. Essa técnica é útil para gerar ideias iniciais e explorar diferentes perspectivas.

Embora práticas, essas abordagens podem ser subjetivas e dependem fortemente da experiência e do contexto em que são aplicadas.

2. Abordagens Quantitativas para Estimativa de Probabilidades

As metodologias quantitativas, por outro lado, utilizam dados numéricos e técnicas matemáticas para calcular a probabilidade de ocorrência de um evento. Elas oferecem um alto grau de precisão e objetividade, sendo preferidas quando há informações históricas disponíveis.

Exemplos de metodologias quantitativas:

• Análise Histórica: Consiste em examinar registros de eventos passados para estimar a probabilidade de repetição no futuro. Por exemplo, em um contexto de segurança, a análise de incidentes anteriores pode indicar padrões de frequência.
• Modelos Estatísticos: Técnicas como regressão, análise de séries temporais e simulações (como o Método de Monte Carlo) ajudam a identificar tendências e prever eventos futuros com base em grandes volumes de dados.

Essas abordagens são ideais para organizações que possuem sistemas de monitoramento ou bancos de dados robustos. No entanto, elas podem exigir mais tempo e recursos especializados.

3. Combinação de Métodos para Estimativa de Probabilidades

Na prática, combinar abordagens qualitativas e quantitativas pode oferecer resultados mais completos e confiáveis. Essa estratégia aproveita o melhor de cada metodologia: a intuição e experiência dos especialistas, somadas à precisão dos dados numéricos.

Vantagens da combinação de métodos:

• Maior Robustez: Permite validar as estimativas qualitativas com análises quantitativas, reduzindo vieses e aumentando a confiabilidade.
• Adaptação a Diferentes Cenários: Enquanto métodos qualitativos ajudam em contextos com dados limitados, os quantitativos fornecem insights em cenários bem documentados.
• Facilidade de Comunicação: Dados numéricos podem ser complementados por explicações qualitativas, tornando as informações mais acessíveis para diferentes públicos.

Por exemplo, em uma avaliação de riscos de segurança, pode-se começar com brainstorming para identificar os riscos e, em seguida, aplicar análises estatísticas para calcular as probabilidades de forma detalhada.

A escolha da metodologia depende do contexto, da disponibilidade de dados e dos objetivos da análise. Seja utilizando abordagens qualitativas, quantitativas ou combinando ambas, o mais importante é assegurar que o processo seja estruturado e alinhado às necessidades da organização. A combinação dessas metodologias frequentemente se destaca como a estratégia mais eficaz para uma estimativa de probabilidades robusta e bem fundamentada.

Escalas de Probabilidade Comumente Utilizadas a Estimativa de Probabilidades

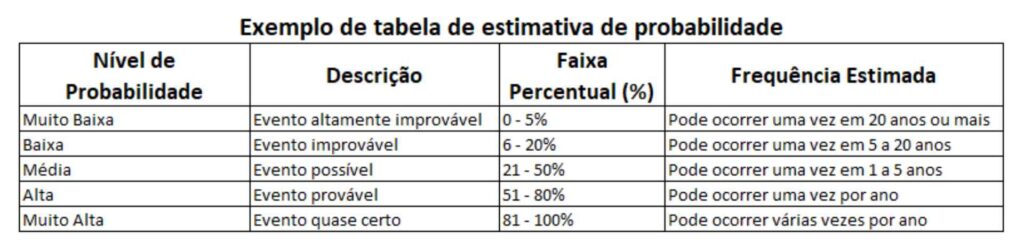
As escalas de probabilidade são ferramentas indispensáveis na avaliação de riscos, pois traduzem o nível de incerteza associado a um evento em termos compreensíveis e comparáveis. Elas ajudam a comunicar a probabilidade de maneira clara e consistente, seja por meio de valores numéricos ou descrições qualitativas. Existem diferentes tipos de escalas, cada uma adaptada a necessidades específicas.

1. Escalas Numéricas

As escalas numéricas são amplamente utilizadas quando se busca precisão na estimativa de probabilidades. Elas atribuem valores objetivos à probabilidade, permitindo comparações claras entre diferentes riscos.

• Escala de 0 a 1: Essa escala representa a probabilidade de um evento, sendo 0 a impossibilidade de ocorrência e 1 a certeza absoluta. Por exemplo, um risco com probabilidade de 0,8 significa que há 80% de chance de ocorrer.
• Escala Percentual: Similar à escala de 0 a 1, mas expressa os valores em porcentagens, variando de 0% a 100%. É particularmente útil para apresentar dados a públicos que preferem uma representação mais intuitiva.
• Escala Logarítmica: Indicada para eventos com ampla variação de probabilidades, como riscos extremamente raros e muito frequentes. Essa escala amplifica as diferenças entre valores baixos e altos, facilitando a análise em situações com grande variação de dados.

Essas escalas são ideais para análises quantitativas e permitem cálculos matemáticos diretos, tornando-as ferramentas preferidas em setores como finanças e engenharia.

2. Escalas Descritivas

As escalas descritivas, por sua vez, utilizam termos verbais ou classificações frequências para representar a probabilidade. Elas são mais subjetivas, mas oferecem maior acessibilidade para equipes multidisciplinares e públicos não técnicos.

• Escalas Verbais: Utilizam adjetivos como “muito baixa”, “baixa”, “média”, “alta” e “muito alta” para descrever a probabilidade. Embora menos precisas, essas escalas são fáceis de compreender e eficazes em situações em que a comunicação rápida é necessária.
• Escala de Frequência: Relaciona a probabilidade com a frequência esperada de um evento. Por exemplo:
  • Nunca: Evento improvável de ocorrer.
  • Raramente: Evento com chances mínimas de ocorrência.
  • Frequentemente: Evento com alta probabilidade de ocorrer.
  • Sempre: Evento praticamente certo.
• Essas escalas são amplamente empregadas em contextos qualitativos, como avaliações preliminares de riscos ou processos de brainstorming.

3. Como Escolher a Escala Ideal?

A escolha da escala de probabilidade adequada depende de diversos fatores, incluindo:

• Natureza do Risco: Riscos complexos podem exigir escalas mais detalhadas, como a logarítmica ou quantitativa. Já os riscos simples podem ser avaliados de forma eficaz com escalas descritivas.
• Disponibilidade de Dados: Em situações onde existem dados históricos ou modelos estatísticos, escalas numéricas oferecem maior precisão. Na ausência de dados, escalas descritivas podem ser mais práticas.
• Facilidade de Compreensão: É fundamental considerar o público-alvo da análise. Equipes técnicas podem preferir escalas numéricas, enquanto gestores e outros stakeholders podem compreender melhor escalas verbais ou percentuais.

Exemplo Prático:

Em um projeto de engenharia, uma escala de 0 a 1 pode ser ideal para calcular a probabilidade de falhas mecânicas com base em dados históricos. Já em um treinamento de segurança, a escala verbal pode ser usada para comunicar riscos de maneira mais intuitiva para a equipe operacional.

As escalas de probabilidade desempenham um papel vital na tradução de incertezas em termos práticos e úteis. Escolher a escala correta é essencial para garantir clareza, precisão e alinhamento com os objetivos da análise de riscos. Seja numérica ou descritiva, a escala selecionada deve sempre facilitar a compreensão e a comunicação entre todos os envolvidos.

Como é Feita a Estimativa de Probabilidades na Avaliação de Riscos?

A estimativa de probabilidades na avaliação de riscos é um processo estruturado que busca determinar a chance de um evento ocorrer, servindo como base para a tomada de decisões estratégicas. Essa etapa é fundamental dentro da gestão de riscos, especialmente quando alinhada às diretrizes da ISO 31000, que fornece um framework internacionalmente reconhecido para identificar, analisar, avaliar e tratar riscos.

Passo a Passo do Processo de Estimativa de Probabilidades na Avaliação de Riscos

Para realizar uma estimativa de probabilidades eficaz, o seguinte processo pode ser seguido:

1. Identificação do Risco: Antes de estimar a probabilidade, é crucial identificar os riscos relevantes. Isso envolve mapear ameaças potenciais que podem impactar os objetivos da organização.
2. Coleta de Informações: Reúna dados pertinentes, como históricos de incidentes, relatórios de desempenho, informações de mercado e insights de especialistas. A qualidade dos dados é determinante para a precisão das estimativas.
3. Escolha da Abordagem: Com base na disponibilidade de dados e na natureza do risco, decida entre abordagens qualitativas, quantitativas ou uma combinação de ambas.
4. Definição da Escala: Selecione uma escala de probabilidade apropriada (numérica, percentual ou descritiva) que melhor se ajuste ao contexto e facilite a comunicação dos resultados.
5. Aplicação de Métodos e Ferramentas: Utilize técnicas específicas para realizar a estimativa de probabilidades, como o Método Hazard Rating Number (HRN), análise de árvores de falhas, ou simulações computacionais.
6. Validação e Ajustes: Revise as estimativas com base em análises cruzadas ou feedback de especialistas para garantir que os resultados reflitam adequadamente a realidade do cenário avaliado.
7. Documentação: Registre o processo e os resultados, assegurando que as informações possam ser consultadas e compreendidas por todos os stakeholders.

Ao seguir um processo estruturado, é possível transformar incertezas em decisões baseadas em evidências, contribuindo para a segurança e a resiliência organizacional.

Exemplos Práticos de Aplicação da Estimativa de Probabilidades

A estimativa de probabilidades na avaliação de riscos é amplamente utilizada em diversos setores, cada um com suas particularidades e desafios específicos. Vamos explorar como essa prática se aplica na gestão de riscos em algumas áreas estratégicas:

1. Setor de Seguros: Cálculo de Prêmios e Reservas Técnicas

No setor de seguros, a estimativa de probabilidades desempenha um papel central no cálculo de prêmios e na gestão de reservas técnicas.

• Cálculo de Prêmios: Seguradoras avaliam a probabilidade de sinistros para definir o valor a ser cobrado dos segurados. Por exemplo, ao calcular o prêmio de um seguro automotivo, considera-se a frequência de acidentes em determinada região, o perfil do motorista e o histórico de uso do veículo.
• Reservas Técnicas: Baseando-se nas probabilidades de sinistros futuros, as seguradoras mantêm fundos reservados para garantir o pagamento de indenizações. Isso é especialmente importante para lidar com eventos raros, mas de alto impacto, como desastres naturais.

2. Setor Financeiro: Avaliação de Crédito e Gestão de Portfólios:

A avaliação de riscos financeiros está profundamente enraizada na estimativa de probabilidades, auxiliando tanto instituições quanto investidores.

• Avaliação de Crédito: Bancos utilizam modelos probabilísticos para calcular a chance de inadimplência de um cliente. Fatores como histórico de crédito, renda e estabilidade empregatícia são analisados para decidir a aprovação de empréstimos ou financiamentos.
• Gestão de Portfólios: Investidores utilizam a estimativa de probabilidades para balancear riscos e retornos em seus portfólios. Por exemplo, ao investir em ações, considera-se a probabilidade de flutuações de mercado para minimizar perdas e maximizar ganhos.

3. Engenharia: Análise de Falhas e Gestão de Projetos

Na engenharia, a confiabilidade dos sistemas e a segurança dos projetos dependem fortemente de estimativas precisas de probabilidades.

• Análise de Falhas: Técnicas como a análise de árvore de falhas ajudam a prever a probabilidade de componentes falharem e a identificar pontos críticos que podem comprometer a integridade do sistema.
• Gestão de Projetos: Ao planejar grandes empreendimentos, engenheiros avaliam a probabilidade de atrasos, estouros de orçamento e problemas técnicos. Isso permite criar planos de contingência eficazes para evitar prejuízos.

3. Saúde: Epidemiologia e Diagnósticos Médicos

No setor de saúde, a estimativa de probabilidades é crucial para prever e gerenciar riscos à saúde pública e individual.

• Epidemiologia: Modelos probabilísticos ajudam a prever a propagação de doenças infecciosas e a eficácia de intervenções, como campanhas de vacinação. Por exemplo, a probabilidade de um surto depende de fatores como taxas de transmissão e densidade populacional.
• Diagnósticos Médicos: Testes diagnósticos utilizam probabilidades para estimar a chance de um paciente ter uma determinada doença com base em sintomas, histórico médico e resultados laboratoriais.

4. Segurança Corporativa: Identificação e Mitigação de Ameaças

Na segurança corporativa, a estimativa de probabilidades auxilia na proteção de ativos, operações e pessoas.

• Identificação de Ameaças: Empresas analisam a probabilidade de ocorrências como invasões, roubo de dados ou interrupções operacionais. Essas estimativas orientam a implementação de medidas preventivas, como reforço de sistemas de vigilância.
• Mitigação de Riscos: Um exemplo prático é o uso de simulações para avaliar a eficácia de um plano de evacuação em caso de incêndio, considerando a probabilidade de diferentes cenários de emergência.

Esses exemplos demonstram a flexibilidade e a aplicabilidade da estimativa de probabilidades na avaliação de riscos em contextos variados. Ao prever eventos adversos e orientar estratégias preventivas, ela garante que empresas e organizações estejam mais preparadas para enfrentar desafios e alcançar seus objetivos com maior segurança e eficiência.

Benefícios da Estimativa de Probabilidades

A estimativa de probabilidades na avaliação de riscos é uma ferramenta essencial para organizações e profissionais que buscam gerenciar incertezas de forma eficaz. A aplicação correta dessa metodologia proporciona vantagens significativas, tornando-se um diferencial estratégico em diversas áreas.

1. Melhoria na Tomada de Decisão: Com uma análise clara das probabilidades, gestores e líderes têm acesso a informações fundamentadas que apoiam decisões mais seguras e estratégicas. Por exemplo, uma empresa pode priorizar investimentos em áreas de maior risco identificado, minimizando impactos negativos e maximizando os resultados positivos.
2. Redução de Incertezas: A probabilidade quantifica incertezas, transformando cenários complexos em informações gerenciáveis. Isso é particularmente valioso em contextos de alta imprevisibilidade, como mercados financeiros ou gestão de crises.
3. Eficiência Operacional: Ao priorizar riscos com base na probabilidade de ocorrência, os recursos podem ser alocados de maneira eficiente, evitando desperdícios e otimizando esforços. Isso é especialmente relevante em setores como segurança corporativa e saúde, onde o uso racional de recursos salva vidas e reduz custos.
4. Fortalecimento da Comunicação: Probabilidades expressas de forma clara, seja em termos numéricos ou descritivos, facilitam o entendimento entre equipes multidisciplinares, gestores e stakeholders externos. Essa clareza melhora a colaboração e o alinhamento entre os envolvidos, aumentando a eficácia do gerenciamento de riscos.

Dicas para Implementar a Estimativa de Probabilidades com Sucesso

A implementação eficaz da estimativa de probabilidades na avaliação de riscos requer uma abordagem estruturada e o uso de boas práticas que garantam precisão, relevância e aplicabilidade dos resultados. Aqui estão algumas dicas essenciais para maximizar os benefícios dessa prática.

1. Utilize Ferramentas Adequadas para Análise: O uso de ferramentas apropriadas é fundamental para garantir que a estimativa de probabilidades seja realizada de maneira precisa e eficiente. Certifique-se de escolher ferramentas que sejam compatíveis com as necessidades e os recursos da organização, equilibrando custo, funcionalidade e facilidade de uso.
2. Envolva Especialistas Qualificados: A experiência humana é indispensável na estimativa de probabilidades, especialmente em situações onde os dados disponíveis são escassos ou quando há necessidade de interpretar contextos específicos. Escolha profissionais com conhecimento técnico e experiência prática no setor relevante.
3. Documente e Comunique os Resultados de Forma Clara: A documentação e a comunicação eficaz dos resultados são etapas cruciais para garantir que a estimativa de probabilidades seja compreendida e utilizada por todos os stakeholders.

Conclusão

A estimativa de probabilidades na avaliação de riscos é um componente essencial para uma gestão de riscos eficaz e estratégica. Ao longo deste artigo, exploramos o conceito, as abordagens, metodologias e aplicações práticas dessa ferramenta, destacando sua importância para diferentes setores, como seguros, finanças, engenharia, saúde e segurança corporativa.

Vimos que a estimativa de probabilidades é crucial para priorizar riscos, tomar decisões informadas, alocar recursos de forma eficiente e comunicar níveis de risco de maneira clara. Abordagens qualitativas e quantitativas, combinadas quando necessário, permitem análises robustas e adaptadas às especificidades de cada cenário.

A importância da estimativa de probabilidades reside em sua capacidade de transformar incertezas em insights acionáveis, proporcionando uma base sólida para decisões estratégicas e mitigação eficaz de riscos. Sua aplicação melhora não apenas a segurança e a resiliência organizacional, mas também contribui para o sucesso de projetos, operações e objetivos de longo prazo.